Beyond the Basics: Demystifying dB
Or: Everything You Ever Wanted to Know About Decibels but Were Afraid to Ask
At first glance, the decibel might seem like an oddly fundamental topic for a series called “Beyond The Basics.” But in practice, the average audio engineer’s understanding of decibels and how they work is often shaky at best.
Granted, you don’t need to fully understand dB to make great-sounding records. But it can never hurt to have a deeper understanding than you already do. Sometimes, going over the underlying theory causes new ideas click, or simmer and synthesize with old ones in the backs of our minds.
Making the Enormous Graspable
Plenty of you may easily remember that dB stands for “deci-bel”, and that this is one-tenth of one “bel” – a fairly obscure unit measurement named after Alexander Graham Bell, a man who is equally famous for inventing the first practical telephone, and for his premature male-pattern chin-baldness.
In essence, the decibel offers a manageable logarithmic scale for measuring changes in level or loudness.
For those who don’t remember too much precalculus, a logarithm essentially allows us to compress large numbers, shrinking the scale of digits down so we can talk about the relationships between them in a more intuitive and graspable way.
dB as a Measurement of Power in Watts
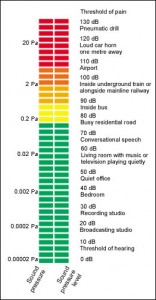
When it comes to loudness, the difference in power between the very quietest sound we can hear and the very loudest that we can stand before feeling pain is a ratio of about one-trillion-to-one.
That’s a 1 followed by 12 zeroes.
Things would get a little awkward and illegible if the numbers written next to our faders went from zero to a trillion, not to mention the cost in ink. So in the 20th century, we settled on dB as the standard measure of volume relationships.
When it comes to acoustic or electrical power (which is measured in watts) dB is easy enough to understand: Every increase of 10 dB corresponds to an increase of 10 times the power, which we tend to hear as a doubling of loudness.
Using this scale, if we were to take the lowest level we can hear and call it “0 dB”, that would make a sound one trillion times more powerful (a level known as our “threshold of pain”) register as “120 dB”.
In other words, if we were to take the quietest sound our ear could hear and label that as 0 dB, then a sound of 10 dB would be 10 times more powerful or twice as loud. 20 dB would be 100 times more powerful or 4 times as loud, 30 dB would be 1,000 times more powerful or 8 times as loud, all the way on up to 120 dB, which would have 1,000,000,000,000 times the power of our 0 dB signal
Adding 120 dB = adding 12 zeroes to the power = 12 increases of 10 dB = 12 doublings in perceived volume.
(At this point, it’s a good idea to hammer home the idea that doubling of power is not the same thing as a doubling in volume. A doubling of power would make for an increase of just 3 dB, which we experience as being just a little bit louder.)
This scale is especially handy for dealing with things like amplifiers, which measure their power in watts.
As you can infer from these numbers, a guitar amp that puts out 100 watts is not 90 times louder than a guitar amp that puts out 10 watts. All things being equal, you might expect it to put out just 10 times the power, and just twice the perceived loudness.
The truth is, it’s sometimes easier and more effective to get more clean level out of an amplifier by switching to a more efficient speaker system than by just upping the brute force of wattage.
dB is also a Measurement of Pressure or Voltage
If the lesson could end here, dB might not seem that complicated at all, and we could all go home for juice and cookies:
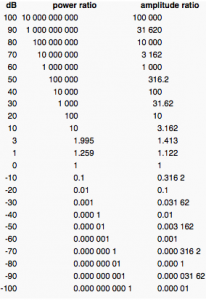
2 times the power in watts = +3 dB = just-a-little-bit-louder.
10 times the power in watts = +10 dB = twice as loud.
100 times the power in watts = +20 dB = four times as loud.
Ok, got it!
Unfortunately, things aren’t quite that simple. This scale changes somewhat when we look at voltage or pressure instead of power.
And in the studio world, we’re actually more likely to use this slightly different, slightly more complex voltage/pressure dB scale.
When we look at the voltage in an analog circuit or the levels in a DAW, things go a little something like this:
2 times the voltage = +6dB
10 times the voltage = +20 dB
100 times the voltage = +40 dB
So, when we’re looking at voltage:… if 0 dB were 1 volt, then 2 volts would be +6dB, 10 volts would be +20 dB, 100 volts would be +40 dB and 1,000 volts would be +60dB.
So, why the two slightly different scales?
Well, Power Law says that Power = Voltage * Current.
And Ohm’s Law (Current = Voltage / Resistance) says that if we increase the voltage of a signal by a factor of 10, we’ll also increase the current by a factor of 10 as well.
This means that an increase in power will basically be the square of an increase in voltage.
This means that increasing the voltage by a factor of 10 should lead to an increase in power by a factor of 100.
Or to put it another way:
10 times the voltage = +20 dB = 100 times the power
Got it?
Maybe read that stuff above one more time. It’ll sink in, I promise.
The math above is pretty neat and tidy, and in the real world things are a bit less perfect. But still, this is the basic fundamental view of how these scales interact. A comparison between these two scales can be found above and to the right.
How Loud of a Difference Can You Hear?
Testing suggests that on average, people experience a tenfold increase in power (+10dB) as a doubling of volume, but keep in mind that this is a subjective measure.
I’ve also heard of tests that suggest people sometimes hear a doubling of voltage (+6dB) as a doubling of volume, and others that say it’s +12dB that sounds “twice as loud.”
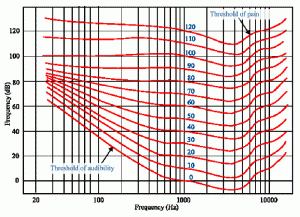
One fact that’s worth acknowledging is that we are not equally sensitive to changes in volume throughout the range of our hearing. It’s said that on average, people can hear changes of about 1dB, up or down, but that depends a bit on what frequency is being tested, and how loud the sound is.
Our ears and brains are more sensitive in the upper mid-range and less sensitive in the bass and highs – although that does even out a bit as we bring sounds up in level overall.
Under the right conditions, even untrained listeners have been shown to hear changes as small as one-half-of-one dB. Trained listeners have even been known to hear as little as a 0.25 dB change, depending on frequency and overall level.
This is a remarkable sensitivity, for sure. But before we slap our own backs for our tremendous ability to hear, let’s take into account a few of our limitations.
Your Hearing is Not Flat
Using electronic devices, we can measure changes in pressure far smaller than those we can hear. And unlike a microphone, which may respond fairly evenly to level changes at different frequencies, our ears are biased toward the midrange – especially when we listen at low levels.
For a low 100 Hz soundwave to sound as loud as a 0dB 1kHz wave, we might need to put about 40 dB of extra energy into it.
But if we were to try to get that same 100 Hz soundwave to seem as loud as a 1kHz tone at 100dB, we might only need to put a handful of extra dB behind the tone.
The takeaway from this is that if you monitor too loud, your mixes can end up sounding a bit weak in the low bass and high, shimmery treble when you play it back at a more normal volume.
dB: A Rolling Log
It’s also important to remember that in and of itself, dB has no value of its own. It’s merely a handy way to measure relationships between two levels. For dB to mean anything at all, we need to assign some concrete value to “0 dB.”
When we deal with SPL, the custom is to make 0dB the quietest sound the average human can hear – an exceedingly infinitesimal pressure of about 20 micropascal.
In digital circuits, we label the loudest sound possible before clipping as 0dBfs (for 0dB “full-scale”) and mark everything else as a negative ratio of that maximum level.
In the analog domain, the custom is to label the ideal operating level as 0dB. Depending on how the meters and circuit are designed this could be a level of 1 volt (dBV) or .775 volts (dBu) or even the power-based standard of 1 milliwatt (dBm).
There has to be some correlation between digital and analog, and often enough, 0dB on an analog VU meter will show up as somewhere between -22dBfs and -16dBfs on a DAW meter depending on calibration, with -18dBfs = 0dB on an analog VU becoming increasingly popular.
There’s another practical takeaway here as well: For the best possible gain staging, it’s often a good idea to record at a level that only reaches only about 2/3 to 3/4 the way up on your digital meters. It’s in this general area that your analog front end is often operating at its best.
Of course, if you like a little more grit, you can always push the input stage of your analog gear harder. But to keep levels well balanced between tracks, and to keep from overloading your master bus or plugins and outboard effects, a little bit of conservative meter-watching at the A/D stage can be just the thing. Especially in 24 bit systems, there’s no reason not to allow yourself a little headroom. Your gear was designed for it.
As always, rules are made to be broken — It just helps when you know what they are first. The rules we’ll always have the greatest difficulty overcoming of course, are the laws of physics. And that is the domain of the dB.
Justin Colletti is a producer/engineer, professor and journalist who lives in Brooklyn. He is a regular contributor to SonicScoop and edits the musician magazine Trust Me, I’m a Scientist.
Please note: When you buy products through links on this page, we may earn an affiliate commission.








James
November 15, 2012 at 9:32 pm (11 years ago)“a guitar amp that puts out 100 watts is not 90 times louder than a guitar amp that puts out 10 watts”
Slightly misleading, since the Wattage of loudspeakers is the rated electrical *input*, not acoustic output power. Since loudspeakers are generally around 1% efficient, one electrical watt of input most definitely does not equate to one acoustic watt of output!
Ben
November 15, 2012 at 10:55 pm (11 years ago)James, what you say is true, but unless you’re going outside the speaker’s frequency response there’s a pretty linear relationship between the amp’s output power and the acoustic power generated by the speaker.
Justin, regarding this bit:
“a guitar amp that puts out 100 watts is not 90 times louder than a guitar amp that puts out 10 watts”
Did you mean 90 times or 9 times? Obviously your point is correct but 90 is a typo, no?
Ben
November 15, 2012 at 10:58 pm (11 years ago)It’s also worth nothing (though for the purposes of making music it doesn’t change the fact that this article is very informative and useful to music types) that technically dB is always a unit-less quantity unless it is referenced to a certain point, such as dBm, dBu, etc. You could look at dB as a unit of difference between two things, or as a representation of a ratio.
James
November 17, 2012 at 1:11 am (11 years ago)You’d be surprised how non-linear it can be, power compression is the biggie, but enclosure types also affect it significantly
Kristian Sharpe
November 20, 2012 at 9:51 pm (11 years ago)Awesome….!
TrustMeI'mAScientist
November 21, 2012 at 4:05 am (11 years ago)Hey Ben, thanks for the feedback.
I suppose I could have written “9 times”, “90 times” or “10 times” in that passage, as each would have identified a potential misconception.
Looking back on it now, I suppose “10 times as loud” might be the most natural and common misconception, and perhaps I should have written that.
Maybe I’ll edit it in the future to clarify that all 3 of these would be misconceptions! “90 times” was just the first of many possible misconceptions that popped into my head.
TrustMeI'mAScientist
November 21, 2012 at 4:10 am (11 years ago)A fair point, for sure, James! The article does qualify that the reality is a little messier than the pure theory, but I thought that this example worked well to show how these ratios scale, all other things being equal.
It is certainly true that a tenfold increase in electrical power may not lead to a pure tenfold increase in acoustic power, and you’re right to mention that. Perhaps a future edit could help make that even more clear than it already is now.
TrustMeI'mAScientist
November 21, 2012 at 4:19 am (11 years ago)I think that bit is actually mentioned in the article, Ben. It states that:
“It’s also important to remember that in and of itself, dB has no
value of its own. It’s merely a handy way to measure relationships
between two levels. For dB to mean anything at all, we need to assign
some concrete value to “0 dB.”
It then goes on to specify the different standards used for dBm, dBv, dBu, dBFS, dB SPL, etc. (That’s all under the fifth subheading, I think.)
My only regret there is that it was awfully redundant of me to put both the qualifiers “in and of itself” and “of its own” in the same sentence! I guess I was really trying to hammer that point home, but still, that was some sloppy style on my part 🙂 If I was writing it again now, I’d surely clean up that sentence.
Derek Martin
November 23, 2012 at 1:16 am (11 years ago)The difference between calculating decibels for power-based quantities and amplitude-based quantities has always bugged me. It seems like most engineers (at least all the ones I have asked) don’t know why it is the case – they just accept it and move on. I really like your explanation here for why power is proportional to the square of voltage – it finally clicked for me after reading this article. Nonetheless, you do not explain why power is proportional to the square of SPL. I’m still trying to understand that.
Sound Spinning
December 1, 2012 at 7:01 am (11 years ago)Total Acoustic power can only be calculated across an enclosure around a sound source. Difficult to measure. And it is the sum of all bits of ac power across the full surface at a distance, say on a sphere. It is then assumed that pressure is constant on this surface and then you can calculate and measure SPL (Sound Pressure Level) at a mic or an ear location. The relationship of ac power as a function of P^2 (press squared) is a mathematical one and not obvious. We (engineers) just know it is the case, but it is maths when you work with the acoustic wave equations on simplified conditions.
On a more practical level:
Sound Power Level (SWL) is dB=10*log(power/power ref); while Sound Pressure Level (SPL) is dB=20*log(P/Pref). So, twice the ac power is +3dB (SWL), and twice the ac pressure level is +6dB (SPL). It’s just pure maths, I’m afraid. If you do the calculations vs listening measurements at 1kHz sine wave sound, then they should all tie up. At other frequencies then you get “Fletcher-Munson curves” to think about, hence possible discrepancies between listening tests and calculations.
Ac power calculations are very interesting because they don’t care about phase cancellations, there is no negative power. However, SPL measurements can be confusing depending on location of mic and frequencies having cancellations, etc. Prone to errors compared to power values, but the noise source is the same.
Phil Dahlen
June 6, 2013 at 4:45 pm (11 years ago)Fine article & good follow-up comments. You mention that : “if you monitor too loud, your mixes can end up sounding a bit weak in the low bass and… etc.” But what is a good widely recommended level. Mention is often made that you should mix and master at 2 different levels, one 12dBs lower than the other. But what is the reference point. I know we don’t all have dB meters lying, but still, if often Googled the question and found nothing convincing. A mention here and there on forums of estimates 85dB for one and 65dB for another. Any ideas anyone ?
PS : I have a feeling I always monitor at too low a level, and in the few studios I’ve worked in, I never found the monitoring too loud, on the contrary but then I don’t do Dub, Dance, Beat or Metal…