Beyond the Basics: Harmonic Motion and the Root of All Music

Music is a rare kind of art form that is made entirely out of vibration. It’s at once both ephemeral and yet inherently physical. We will never be able to reach out and grab it in our hands, but it certainly touches us in the most literal sense of that word. If you’re feeling poetic, you might even compare hearing itself to a specialized, hyper-sensitive form of touching; one that works across great distances.

Most of us already have some cursory understanding of how sound works. If you’ve gotten through most of high school, you probably know that sound travels as waves through air, liquids and solids. But it’s rare that we stop and think about exactly what that means, and what it implies. That’s unfortunate, because only by understanding this concept fully can we unlock the knowledge that’s key to clearing up some of the most pervasive questions and misunderstandings around sampling rates, room acoustics, equalizers – even about where music comes from and why it can be so mesmerizing.

If there’s a basic building block of all music and sound, it’s harmonic motion. Acoustician Dr. Dan Russel of Penn State  has created dozens of free educational animations that help explain these concepts, and makes them available to the public on his site. I use them regularly in teaching my college courses on audio. One of my favorites is among his simplest:

Wave Animation

I could watch this thing all day.

To the left is a diaphragm – like a speaker, or the soundboard of a guitar.

As it vibrates, it pushes forward, compressing the air molecules. Then, it pulls back, rarifying the air. Repeat this back-and-forth movement enough times in a second and we have a frequency of motion that registers on the ear as sound.

At first glance, your eye may be tempted follow the movement of the wave, itself, from left to right: “Aha!” you might think. “So, these columns of compressed air molecules travel forward, emanating from the speaker, until they arrive at my ear, one after the other!”

But physics is often counter-intuitive, and that’s just not the way it works. The air molecules do not really travel from the speaker to your ear. That would be called “wind.” Instead, each one of those molecules just kind of hangs out around a general home-base and simply moves back and forth, back and forth. Almost like a pendulum.

Go on, scroll back up and take another look. But this time: don’t focus on the wave.

Instead, look at one single particle. Trace its movement with your finger.

Do you see him there, just kind of hanging out? Going back, and forth, back and forth, back and forth, like a little metronome?

That’s harmonic motion.

Newton’s Cradle

Instead of an original molecule from the left making it all the way to your ear, the force of the initial vibration moves from one molecule to the next, a bit like the executive’s clacking-ball toy, “Newton’s Cradle”.

(Except in the case of air molecules, they’re spread out, and they don’t physically collide. When they get too close, they actually repel each other. But that’s topic enough for a whole ‘nuther article.)

Much like a pendulum, the speed at which each molecule moves back and forth is not constant. When a pendulum, a speaker or a molecule nears the end of its “swing” in one direction, it becomes chock full of potential energy and, eager to fly in the opposite direction, accelerates towards center.

As it passes through the central resting point, it still has plenty of energy left and keeps on moving, gradually slowing down until it reaches the final extreme on the other side. There, with no energy left to keep going forward, and a bunch of new potential energy on board ready to steer it the other way, it begins hurtling back toward center again.

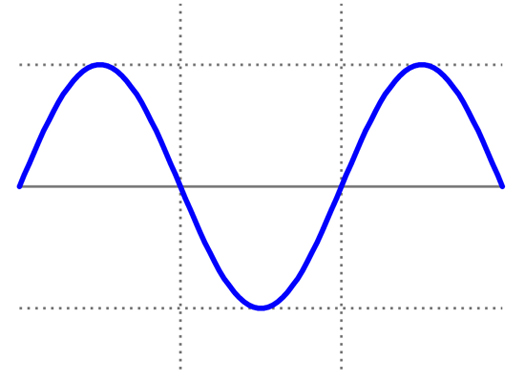
Graph out this kind of gradually changing speed on a piece of paper, and you’ll have a very familiar image. It looks a little something like this:

Simple sine wave

Ah, the sine wave. This natural speeding up and slowing of harmonic motion is what give its undulating wave shape. If the speed were constant, we could draw it with straight lines, like a triangle. But that’s just not how vibration, and harmonic motion, work.

Charts like these are not to tricky to understand. If we track the movement of any individual molecule, the “up” position on this graph would represent the molecule moving as far as it can to the right, the fully “down” position would indicate movement as far as possible to the left.

From here on out, things get a little “meta”. We can zoom out and look at the wave itself. “Up” represents compressed air, “down” represents rarefied air. Or we can look at the movement of the speaker: “Up” on this graph means speaker pushes out, “down” means speaker pulls back in. In an analog system, this same image could be used to indicate the fluxuation of voltage in a circuit, the change in magnetism on a piece of tape, or the ins and outs of the groove on a vinyl record.

Digital systems are a little different. To recreate this wave perfectly, all we need to know is where the molecule has been at more than two points in each cycle. From there, knowing what we do about the laws of harmonic motion, we can extrapolate where that molecule was between each of those points. Despite popular misconception, this sine wave would not be awkwardly mangled and re-drawn as a triangle or square wave. We know how molecules accelerate and decelerate. This is math that we can do. It is not an unknown.

Of course, the animation above is a bit simple. First of all, sound propagates in all three dimensions, not just in just one direction as we have here. By it’s very nature, sounds wants to be “omnidirectional.” It is only through concerted design that we can we can effectively channel it one way or another. The stuff doesn’t simply go left-right, or even center-out. It vibrates every damn way it can.

But even though sound waves are a bit more complex than this in practice, this same fundamental kind of movement is still at play. In the early 19th century, a scientist named Joseph Fourier helped lay the groundwork for understanding that all complex molecular motion is basically built out of layers upon layers of these simple harmonic motions. More complex sounds – from the relatively pure tone of a flute to the overdriven chords of an electric guitar – are made out of what might be described as thousands of discrete sine waves – some of them harmonically related, some not.

Vibrating String

A pure sine wave, where all molecules move back and forth together in perfect sync, is practically impossible to recreate in nature. Instead, what we get is a blend of molecules moving at different rates and at different times. We can see this effect in the motion of a guitar string, which does not vibrate at only one rate – but at several rates at once.

When we pluck the low E string on a bass guitar, we hear not only the “fundamental” pitch of about 80 Hz, but also mathematically-related harmonic overtones at 160 Hz, 240 Hz, 320 Hz, 400 Hz, 480 Hz, 560 Hz, 620 Hz and so on. (It’s actually more like 82.4 Hz and up from there, but I’ll spare you the awkward decimals.) In essence, only thing that separates this low E from the same E on a piano are the durations and proportions of these additional, harmonically-related vibrations.

What’s especially amazing about the relationship between fundamental pitches and their harmonic overtones is how, through natural law alone, they routinely fall in and out of phase with each other. This natural synchronization of vibration is what makes instruments sound so beautiful on the ear. And when you visualize it, the effect can be just as stunning:

Ok, now this I could really watch all day.

What you’re seeing here is the visual equivalent of a single, very pure note in action.

The longest of these pendulums is like the fundamental pitch, and the following pendulums are scaled proportionately shorter and faster, in essentially the same way that harmonic overtones are. This is music in motion.

On a real-world instrument, we’ll get some unrelated “enharmonic” overtones as well. These  “impure” resonances are especially prevalent in instruments like distorted guitars, snare drums and wood blocks.  In great doses they will obscure our sense of pitch. But these unrelated overtones are just part of makes instruments sound so damn interesting.

When we EQ sounds or treat instruments, we’re playing with these overtones – their proportions and their durations. It’s almost like creating alternate “timbres” of the mesmerizing visual pattern above by launching different pendulums at different times or from different heights; by futzing with the mathematical purity of their length; by repressing the movement of some pendulums and not others; by introducing unrelated “enharmonics”; or by making some pendulums more visible than others through changes in lighting.

Our relationship with this natural “harmonic series” is so ingrained that you can leave out the bottom pitch, and our minds will automatically fill it in. This is precisely what happens with smaller pianos, which often have soundboards too small to reproduce the deepest fundamentals.

Our ears might not “hear” the low fundamental in a literal sense, but our brains sure do. You can even try it yourself with a sine wave generator: Play your brain 110 Hz, 165 Hz, 220 Hz, 275 Hz, 330 Hz, 385 Hz, 440 Hz all at once and it will instantly go “Oh! I get it. 55 Hz. Low A,” and will fill it in without you doing a thing about it. You can’t help but hear the phantom fundamental.

This harmonic series isn’t just where tone comes from. In it lies the very foundations of all music. If you were to play these overtones together at equal intensity, you would basically get a chord like this one:

(On piano, it would sound something like this.)

These first harmonics give birth to the western 8-tone scale. And if you zoom in on only the first, most prominent handful of these overtones, you have the raw ingredients to re-create the near-universal 5-note pentatonic scale. The truth is that the full vocabulary of music comes baked right into every note. It’s almost fractal in a way.

The appeal of these natural relationships – which stem from simple molecules vibrating in and out of phase – is inescapable for us. Bobby McFerrin demonstrates just how ingrained this series is, by using it to hack your brain:

It’s easy for us to lament the kids these days with their digital downloads and their streaming. Back in the days when tape and vinyl ruled, the stuff had substance, it had weight, it had tangibility. But to feel this way is to mistake the medium for the message.

There may always be a place for manufactured accessories to music, but for most of human history, we have experienced music not as a material product to be loaded on to tractor-trailers, but as pure vibration in the air. However we consume it, music will always be as physical as it is fleeting. It is as real as the matter around us, and as impossible to bottle as a stroke of lightning. The best we can do is to create devices that will measure it and approximate it in another form, whether that be the etchings on a wax cylinder or the ones and zeros of a solid-state hard drive.

Until we can tap audio straight into our neurons, we will always need to make molecules move in order to hear the stuff. In this way, music is, and likely always will be, an ever-evolving game that we play with the physical, natural world.

Justin Colletti is a mastering engineer who writes about the art, science and economics of music and sound.

Please note: When you buy products through links on this page, we may earn an affiliate commission.